控制器设计概述
机器人工程师工种:
- 机器人编程员 Robot programmers usually start with a robot that has controllable joint or end effector positions. If you are a robot programmer, you are probably implementing motion planning algorithms and integrating the manipulator with other software components, such as perception and decision-making.算法设计和感知、决策模块的软件开发
- 机器人设计师 Robot designers have a goal of enabling robot programmers. If you are a robot designer, you need to deliver a manipulator that can safely and reliably accept joint or end effector commands. You will likely apply some of the control design techniques discussed in this post and implement these controllers on embedded systems.安全可靠地接收控制指令、执行控制指令、嵌入式系统设计
Of course, nothing is quite as rigidly separated in real life. Chances are that robot manufacturers will provide their own controllers, but may also decide to expose control parameters, options, or maybe even a direct interface to the actuator torques.生产制造商可能会提供自己的控制器,但是也需要开发控制参数、控制选项或者与驱动器力矩直连的接口信息。
从运动学到动力学
回顾上一部分,运动学把机器人操作臂的关节位置映射为末端执行器的位姿。动力学,则是把所需的关节力和力矩映射为关节位置,速度和加速度。

动力学需要掌握操作臂更多的机械特性,具体包括以下惯性性质:
- 质量(mass)
- 惯性张量(inertia tensor):一个3x3由惯性矩(moments of inertia)和惯性积(products of inertia)组成的反对称矩阵
- 质心(center of mass):如果质心不在定义的坐标系上,需要通过平行移轴定理把绕质心的旋转转变为绕已定义坐标系的旋转。
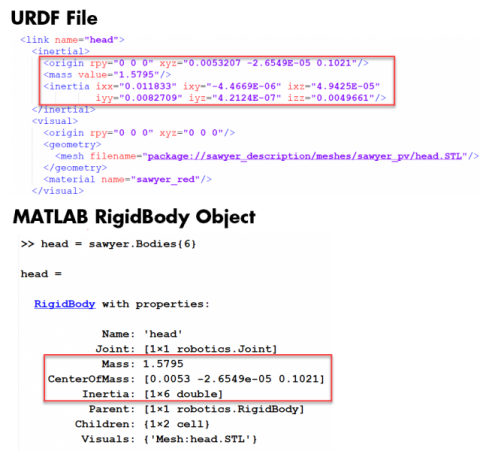
通常,通过导入URDF文件加载已有的操作臂模型时,上述的惯性性质已经自动定义在URDF文件中了
控制关节力/力矩
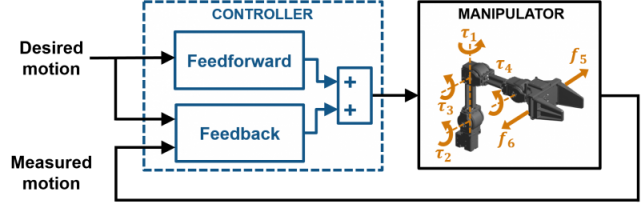
机器人操作臂的运动控制器一般由以下两部分组成:
- Feedback: 同时输入期望的运动和测量到的实际运动信息计算得到关节输入,通常涉及某种控制律,使得期望的运动和测量到的实际运动之间的误差最小。
- Feedforward:只输入期望的运动计算关节输入,通常涉及应用操作臂机械学模型来计算开环输入。
In our video “Controlling Robot Manipulator Joints”, we explore two different examples of joint controllers, featuring the 4-DOF ROBOTICS OpenManipulator platform. You can also download the example files from the MATLAB Central File Exchange.
Controller Example1:Inverse Kinematics + Joint Space Controllers
First, **inverse kinematics(IK)**被用来将末端执行器的参考位置转换成一系列的参考关节角度。然后运动控制器专门运行在关节角度配置空间(in the configuration space),也就是运行在关节位置上。
- Feedforward前馈部分在操作臂模型上应用逆向动力学,这个操作可以计算出所需要的关节力或力矩,让操作臂跟随期望的运动,同时也==补偿了重力==。
- Feedback反馈部分使用PID控制方法。每个关节(4个旋转关节+夹爪工具)都有各自独立的控制器以使得期望的运动和测量的实际运动之间的误差最小化。
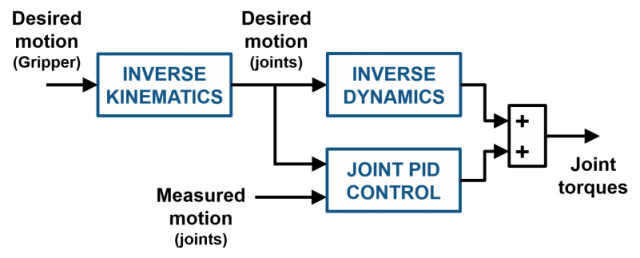
为了使轨迹光滑,我们通常需要与曲线方程类似的封闭式的轨迹,这是因为逆向动力学需要用到操作臂的位置,速度和加速度来计算所需要的关节力或关节扭矩。因此,生成一个可微分的曲线参考轨迹就容易实现上述要求。
理论上,逆向动力学就足够控制机械臂运动了。但是,考虑到存在一些因素,例如关节机械特性(例如刚性,阻尼和摩擦等)、无法测量的扰动、驱动器或传感器噪声、甚至是数值计算误差,这些因素很容易影响开环控制器的鲁棒性。因此,需要加入额外的反馈补偿。
前馈和反馈控制部分是相对容易操作执行的而且不太耗费计算能力,因此关键控制结构还在逆向运动学求解。正如在机器人操作臂第一部分:运动学中所言,逆向运动学求解器(inverse kinematic solver)采用的是数值法求解IK,因此会需要大量的计算。这种情况可以通过给定一个优良的初始状态估计(通常是前一个测量的实际运动),限定迭代的最大次数或者转为解析求解方法来解决和改善需要大量计算的情况。
Controller Example 2: Task Space Controller
第二种运动控制的方法运行在任务空间,也就是运行在末端执行器的位置和姿态之上。这避免了使用几何雅可比(geometric Jacobian)求解IK问题。
几何雅可比 geometric Jacobian是操作臂关节角度/位置构型$\mathbf{q}$的函数。通常写作$\mathbf{J(q)}$.雅可比矩阵将关节空间的关节角速度映射成末端执行器相对于基坐标系的速度(角速度和线速度),关系如下
$$
^0v_{ee}=\begin{bmatrix}
^0v\
^0\omega
\end{bmatrix}=\begin{bmatrix}
v_x\
v_y\
v_z\
\omega_x\
\omega_y\
\omega_z
\end{bmatrix}=^0J\dot q=^0J\begin{bmatrix}
\dot q_1\
\vdots \
\dot q_n
\end{bmatrix}
$$
雅可比矩阵也可以把关节空间的关节力或关节扭矩映射到末端执行器世界坐标系下的力和力矩,关于雅可比Jacobians详细介绍,可以参考这篇博文:ROBOT CONTROL PART 2: JACOBIANS, VELOCITY, AND FORCE
任务空间的运动控制方法
- Feedforward前馈部分只需对重力进行补偿
- Feedback反馈部分对末端执行器的XYZ位置进行PID控制(we ignore orientation here, but you really shouldn’t!)用以计算末端执行器世界坐标系下所期望的力和力矩.然后,雅可比逆矩阵将(PID)控制输出转换成关节空间的关节力或关节扭矩
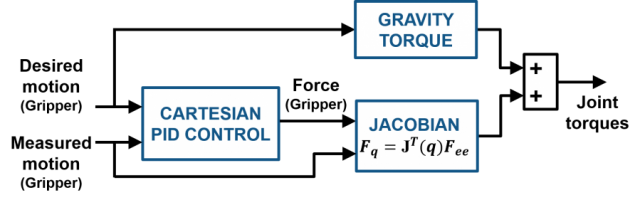
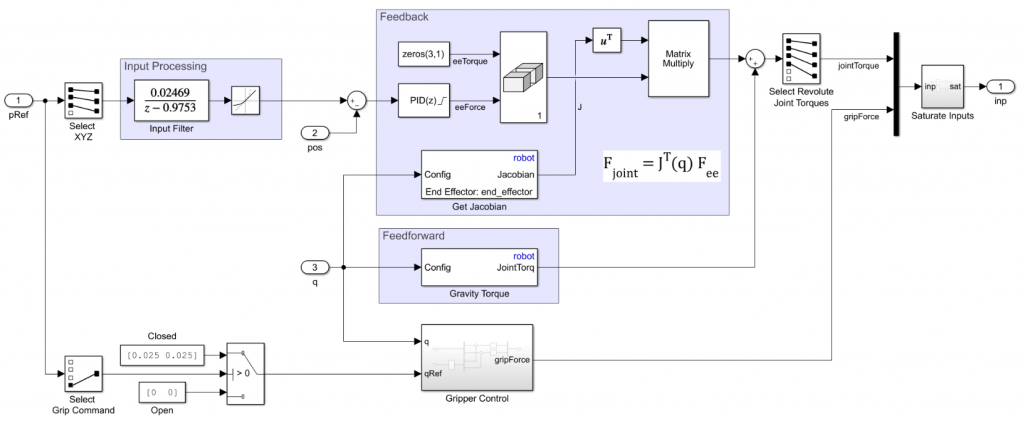
以下是任务空间运动控制示例的运动控制器截图,不像上面的方案,控制器Simulink模型包括其他的实际因素,例如滤波器、速率限制器、饱和输入(Saturate Input)和带有基本逻辑的解耦的夹爪工具。 You can download this model from the MATLAB Central File Exchange.
控制方法的调研
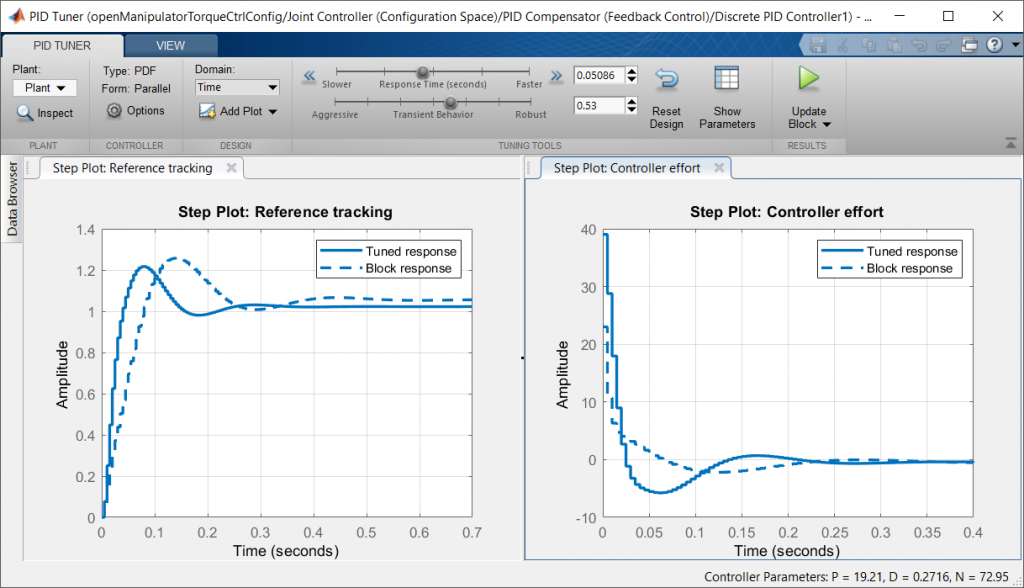
Once you have a model of your manipulator, there are many tools in MATLAB and Simulink that can help you design joint controllers.
- PID Tuner PID调参器 for single-input single-output(SISO) compensators
- Control System Designer 控制系统设计器和 Control System Tuner 控制系统调参器 for multi-input multi-output(MIMO) systems
- MPC Designer模型预测控制设计器 for model-predictive controllers
传统控制涉及依赖于线性化 linearization或者依赖于找到非线性模型关于某个特定操作点(比如the “home”, or equilibrium, position of the manipulator)的线性近似。A controller designed about an approximate linear region can become less effective, and potentially unstable, as the robot state deviates from that region.围绕近似线性区域设计的控制器很可能是无效和不稳定的,因为机器人状态会偏离哪个近似线性区域。这种情况可以通过考虑测量到的系统实际状态(在本例中,是关节位置或末端执行器的位置)的非线性控制技术解决。前馈技术比如反向动力学或计算几何雅可比,可以保证控制器解决非线性问题。另一个普遍的技术是增益调节(gain scheduling),它可以应用于传统控制器 traditional controllers和模型预测控制器 MPC controllers。
也可以应用下列不基于模型的其他方法:
- Optimization优化: 可以通过Simulink控制优化工具箱 Simulink Design Optimization的仿真优化控制参数。尽管优化的方法不会保证稳定性,但是它允许你自动调节一系列参数,例如增益、力或速率极限值,阈值等,这些都可以带来良好的结果,尤其是对于高阶非线性系统。
- Machine Learning机器学习: 强化学习或者是通过实验和错误的自动式学习,是应用在机器人操作臂上一项常见技术。For example, this paper and video shows deep reinforcement learning——换言之,使用强化学习方法的深度神经网络的参数学习方法
总结 Conclusion
Now you’ve seen an overview of kinematics and dynamics for robot manipulator design. I hope this was a useful introduction to the language in this domain, some common techniques used in practice, and areas where MATLAB and Simulink can help you design and control robots.现在,你对机械臂的运动学和动力学设计有所概览。我希望这是对专业领域、实际应用技术领域的有用介绍,并且希望通过使用MATLAB Simulink,能帮助你控制机器人。
We hope that Simulink can help you during your design phase as you explore different architectures, integrate supervisory logic, perform tradeoff studies, and more. Also, recall that Simulink lets you automatically generate standalone C/C++ code from your control algorithms, so they can be deployed to hardware or middleware such as ROS.我们希望通过Simulink能帮助你设计,探索不同的逻辑架构,集成监督逻辑,进行协调平衡学习等。Simulink还支持对控制算法自动生成标准的C/C++代码,有利于在硬件环境以及像ROS等中间软件上部署代码。
If you want to see more material on robot manipulation, or other topics in robotics, feel free to leave us a comment or email us at roboticsarena@mathworks.com. I hope you enjoyed reading!
– Sebastian
Reference
MATLAB Blog Racing Lounge - Robot Manipulation,Part 2:Dynamics and Control
「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
